合肥市新东方在职考研英语班一览
发布:留学小助手 时间:2025-04-29 16:12 点击:456
合肥市新东方在职考研英语班一览
合肥市新东方在职考研英语班一览新东方考研2025考研全科半年无忧计划:该课程是针对考研公共课和考研专业课开创的全方位辅导体系。全程封闭式管理、星级教学住宿环境、高三式密集课程安排、小班课程教学、考研经验教师驻营面授精讲、传授解题技巧、全程跟进答疑、助教严格督学,帮助学员攻克考研重难点。通过系统学习,借力新东方教师丰富教研经验,明晰考试体系,复习重点;建立科学、自主、高效学习方法,为后续学习打下坚实基础、逐级提升,层层突破,最终在考试中脱颖而出。通过高级学管师1V1评估指导,定制专属适配院校规划方案,不盲目从众,明晰备考目标,实现精准备考。通过系统全面细致的伴学体系,及时解决问题,扫清盲点。...

新东方考研辅导班
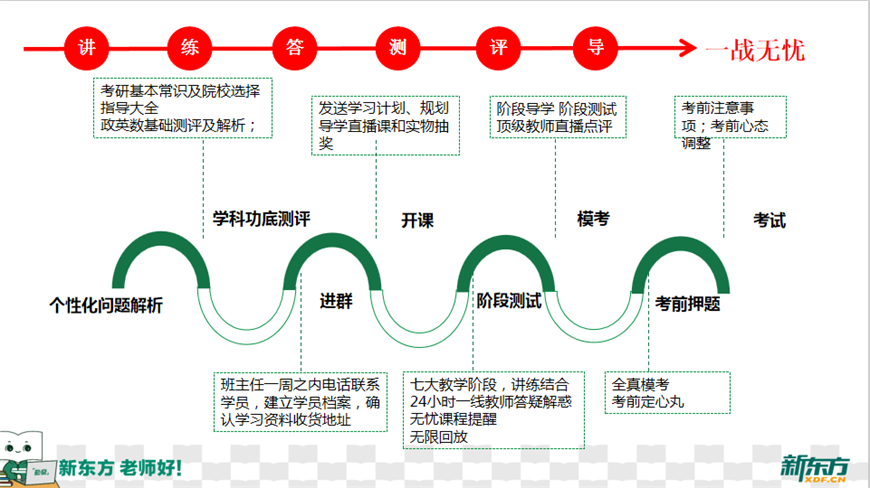
合肥市新东方在职考研英语班一览新东方考研培训班系统化教学方案;导学入门:考情分析,重点梳理,搭建学科只是体系。基础夯实:考点精讲,讲练结合,强化吸收,加深理解。专项强化:知识点归纳、对比,提升知识综合运用能力。真题突破:精析真题,把握脉络,掌握出题意图及得分技巧。冲刺点睛:模拟刷题,查漏补缺,题海突围。辅导答疑:每日知识串讲、测评答疑、作业批改、规划指导、学习督促。

新东方考研九大专业单独开班
-

199管理类综合班
勤搬金砖 发家致富
-

396经济类联考班
锁定高校 稳拿高薪
-

金融专硕(数三)班
打破局限 拓宽视野
-

计算机定向班
巧借东风 崭露头角
-

翻译硕土定向班
翻译官? 你也可以!
-

艺术硕土定向班
艺苑人生 完美定格
-

法律硕土定向班
法政先锋 携梦前行
-

临床医学定向班
不辞艰辛 执着坚定
-

经济学定向班
高端大气 有财多金
新东方考研无忧计划

新东方考研无忧计划教学四大优势
-

制定辅导方案
我们通过对历年考研学生的跟踪研究形 成大数据系统,深刻剖析深层原因如:数学 差的同学,有可能是因为逻辑思维跟不上, 可能是因为理解能力不足,也可能是因为记 忆力差...对于每一类的同学,我们都有针对 性的备考方案。
-

反转式课堂理念
是该对抹杀考生积极性填鸭式教学说 再见了,您可以随时随地,每一节课,每 一个自习与讲师进步互动教学,互动 答疑。您可以随时提出问题,然后以问题 为核心展开讨论。
-

切片式教学稳步强化
通过数据整合,我们总结出2000多个重 难点切片,并将这些重难点分为四个学习阶 段:基础阶段,强化阶段,实战阶段,冲刺 阶段。针对学员每一阶段的学习状况我们都 有针对性的考点讲解。
-

师资参与服务中
考研集训营重大升级之一,即集训 营所有的课程,都有授课老师参与教学服务, 即时为学生解决学习中的问题;且公共课 配有自己全职师资,20大热门专业课配有自己 全职师资。

新东方考研网是专业考研网校,为您提供线上线下考研培训班、考研辅导班、考研网络课程,以及最新的考研报考、考研备考、考研真题解析、考研复试调剂等资讯信息。更多考研问题可在线或者电话咨询专业老师了解详情
新东方考研培训班分享
考研数学证明题技巧
结合几何意义记住基本原理
重要的定理主要包括零点存在定理、中值定理、泰勒公式、极限存在的两个准则等基本原理,包括条件及结论。
知道基本原理是证明的基础,知道的程度(即就是对定理理解的深入程度)不同会导致不同的推理能力。如2006年数学一真题第16题(1)是证明极限的存在性并求极限。只要证明了极限存在,求值是很容易的,但是如果没有证明第一步,即使求出了极限值也是不能得分的。
因为数学推理是环环相扣的,如果第一步未得到结论,那么第二步就是空中楼阁。这个题目非常简单,只用了极限存在的两个准则之一:单调有界数列必有极限。只要知道这个准则,该问题就能轻松解决,因为对于该题中的数列来说,“单调性”与“有界性”都是很好验证的。像这样直接可以利用基本原理的证明题并不是很多,更多的是要用到第二步。
借助几何意义寻求证明思路
一个证明题,大多时候是能用其几何意义来正确解释的,当然最为基础的是要正确理解题目文字的含义。如2007年数学一第19题是一个关于中值定理的证明题,可以在直角坐标系中画出满足题设条件的函数草图,再联系结论能够发现:两个函数除两个端点外还有一个函数值相等的点,那就是两个函数分别取最大值的点(正确审题:两个函数取得最大值的点不一定是同一个点)之间的一个点。这样很容易想到辅助函数F(x)=f(x)-g(x)有三个零点,两次应用罗尔中值定理就能得到所证结论。
逆推法
从结论出发寻求证明方法。如2004年第15题是不等式证明题,该题只要应用不等式证明的一般步骤就能解决问题:即从结论出发构造函数,利用函数的单调性推出结论。
以上就是一些考研不等式的证明方法的相关建议了,希望能够帮助到大家!
专注:合肥市新东方在职考研英语班一览 在线咨询
